De Broglie Wavelength Calculator

Rest Mass(kg):

Velocity:

Momentum (p):

Wavelength (λ):

What is the de Broglie Equation?

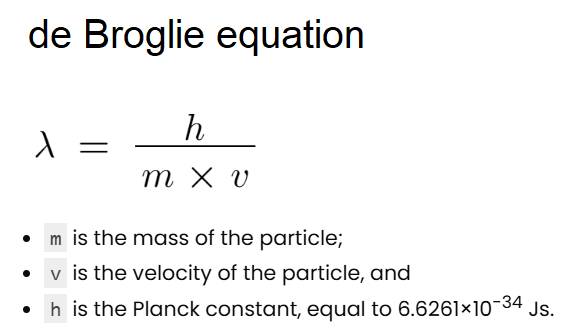
According to de Broglie, a beam of particles of some mass can behave as a matter wave. Its wavelength is related to the mass and velocity of the particle:

λ = h / (m × v)

where:

m is the mass of the particle;
v is the velocity of the particle;
h is the Planck constant, equal to 6.6261×10^-34 Js.

The Units of Mass

The mass of particles is usually given in kilograms, but using scientific notation since the numbers are small. The value of the electron rest mass (m_e) and the atomic mass unit (u), which is an average of the proton and neutron masses, are:

1 m_e = 9.10938356 × 10^-31 kg
1 u = 1.660538921 × 10^-27 kg

What is the de Broglie Wavelength of an Electron?

Let's find the de Broglie wavelength of an electron traveling at 1% of the speed of light.

The mass of an electron is 1 m_e, or 9.10938356 × 10^-31 kg.

The speed of this electron is 299,792,458 m/s / 100 = 2,997,924.58 m/s.

Multiplying the mass and speed, we obtain the momentum: p = mv = 2.7309245 × 10^-24 kg·m/s.

Dividing the Planck constant by p, we obtain the de Broglie wavelength: h/p = 6.6261 × 10^-34 / 2.7309245 × 10^-24 = 2.426 × 10^-10 m.

Hence, the de Broglie wavelength of our electron is 0.24 nm.

How to Calculate the de Broglie Wavelength of a Photon?

Since a photon's rest mass is zero, you might wonder how to use our de Broglie wavelength formula to find the de Broglie wavelength of a photon. Thanks to wave-particle duality, a photon does have a momentum associated with it. The value of this momentum can be used to calculate the de Broglie wavelength of the photon.

A question asks you to find the de Broglie wavelength of a photon which has a momentum of 6.8 × 10^-35 kg·m/s. Let's see how to use our calculator to answer this question:

Click on the unit changer menu of the momentum row and select x10^-35 from the list.
Enter 6.8 into the momentum row.
You will see the result for the wavelength in nanometers by default. Change the units to meters for a more manageable value. The result is 9.74 m, rounding to 3 significant figures.

FAQs

What is the unit of the de Broglie wavelength? The unit in which the de Broglie wavelength is expressed is meters. Since the de Broglie wavelength is usually very small, we most often express this value in nanometers.

How do I calculate the de Broglie equation? To determine the de Broglie wavelength of a particle given its mass and velocity, you need to:

Multiply the velocity by mass. Their product is the particle's momentum.
Divide Planck's constant by the momentum found in Step 1.
The result is exactly the de Broglie wavelength of your particle.