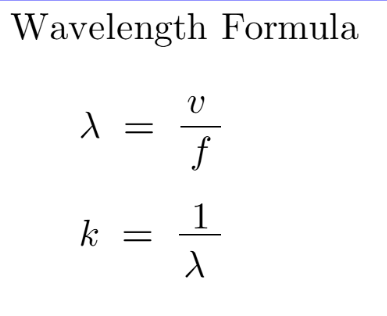
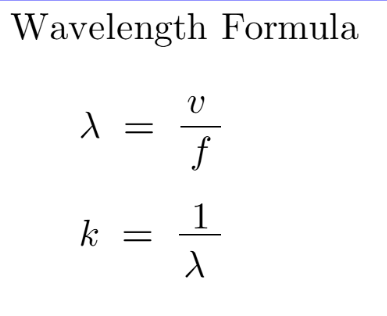
A Wavelength Calculator is a tool used to determine the wavelength (\( \lambda \)) of a wave based on inputs such as the wave's frequency (\( f \)) and the speed of the wave (\( v \)). The wavelength is the distance between two consecutive points of the wave, such as two peaks or troughs. This calculator is commonly used in various fields like physics, telecommunications, and acoustics.To use this calculator, you need to provide the frequency of the wave in Hertz (Hz) and the speed of the wave in meters per second (m/s). Depending on the type of wave (e.g., sound, light, electromagnetic), the speed may vary. For light waves in a vacuum, the speed is typically the speed of light (\( c = 3.00 \times 10^8 \) m/s), while for sound waves, the speed can depend on the medium (air, water, etc.).Once the frequency and wave speed are entered, the calculator will calculate the corresponding wavelength, helping you understand the characteristics of the wave, such as its energy or behavior in different media.
There are three main properties of a wave: its velocity, wavelength, and frequency.
Wave Velocity (v)Wave velocity is how fast a wave propagates in a given medium. Its unit is meters per second (m/s).
Wavelength (λ)Wavelength is the distance over which the shape of a wave repeats. It depends on the medium in which a wave travels and is measured in meters (m).
Frequency (f)Frequency refers to how many times (per second) the particles of a medium vibrate when the wave passes through it. The unit of frequency is Hertz (Hz) or 1/s.
The relationship between wavelength and frequency is described by the equation:
Make sure to use the proper units! If needed, you can always convert speed values.
Here are some common wave velocity values:
The general wave equation that relates wavelength, frequency, and wave speed is:
\( v = f\lambda \)
For electromagnetic waves traveling in a vacuum, the relationship is:
\( c = f\lambda \)
The formula for the de Broglie wavelength of a particle is:
\( \lambda = \frac{h}{p} \)
The wavelength of light in a medium with refractive index \(n\) is given by:
\( \lambda_m = \frac{\lambda_0}{n} \)
The energy of a photon in terms of its wavelength is given by:
\( E = \frac{hc}{\lambda} \)
The Bragg's law for X-ray diffraction is:
\( n\lambda = 2d\sin\theta \)
The best wavelengths of light for photosynthesis are blue (375-460 nm) and red (550-700 nm). These wavelengths provide the right energy to excite electrons in plant pigments, which is essential for photosynthesis.
They are inversely proportional: fλ = c, where c is the speed of light. If frequency increases, wavelength decreases, and vice versa.
Red (~700 nm) has the longest visible wavelength. However, radio waves have even longer wavelengths, but they are not visible to the human eye.